Best Low Risk Investments in Canada Right Now (May 2025)

Written by: Jordan
With so many threats to our economy in 2025 many Canadian investors are looking for low risk investments.
Personally, I recommend that if you plan on using your cash within the next five years, it’s worth sticking to investments covered by the Canadian Deposit Insurance Corporation (CDIC). High-interest savings accounts and GICs (Guaranteed Investment Certificates) fall under this umbrella. They’re not flashy, but they’re safe.
On the other hand, if you’re looking to build your nest egg for a goal five or more years down the road (retirement being the most prominent example) then taking a peek at my article on the best long term investments in Canada may be the better call.
Below, you’ll find a list of the top low-risk investments in Canada. It’s meant for anyone saving up for a down payment, setting aside funds for an upcoming vacation, or maybe planning to buy a new car in the next couple of years.
Just remember, while many low-risk options share common traits – such as relatively steady growth and minimal volatility – there are still important differences between them. So, don’t forget to do a little comparison shopping before committing to make sure you find the perfect fit for your goals. Specifically, I recommend making sure that you know exactly how long your money will be locked into an investment for, or what the penalties would be if you had to get it out in a hurry.

Best 2025 Broker Promo
Up to $150 Sign Up Bonus!
Open an account with Qtrade and get the best broker promo in Canada: $150 in cash back when you fund a new account.
The offer is time limited - get it by clicking below.
Must deposit/transfer at least $1,000 in assets within 60 days. Applies to new clients who open a new Qtrade account by October 31, 2025. Qtrade promo 2025: CLICK FOR MORE DETAILS.
Best Safe Investments Compared
When most people look for the best low risk investment opportunities available to them, they define risk as the possibility of losing part or all of your capital (the initial sum of money that you put into an investment). I think that’s a reasonable definition. Long story short – most people don’t want to lose their hard earned money!
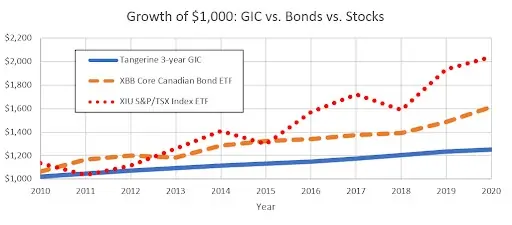
Here’s a quick chart outlining the various low risk options available to Canadian investors. When we refer to risk level in this chart we’re not referring to return risk. What we’re referring to is safety from potential fraud or bankruptcy of the underlying company. For example, if you have your money in a high interest savings account or GIC with a bank, it is guaranteed by CDIC insurance (the government) up to $100,000 per account.
| Investment Product | Risk Level | Average Returns | Best Source |
| HISAs | Guaranteed by government | 4% | EQ Bank |
| GICs | Guaranteed by government | 3.45% for 1 year | EQ Bank |
| T-bills | Guaranteed by government | 3-4.07% | Qtrade |
| Money Market Funds | Returns are not guaranteed | 2.77-3.24% | Qtrade |
| Corporate Bonds | Returns are not guaranteed – but are safer than stocks | Varies | Qtrade |
| Government Bonds | Guaranteed by government | 3% | Qtrade |
| Annuities | Guaranteed by law | Varies | Insurance professionals |
| Low risk stocks | Returns are not guaranteed | Varies | Qtrade |
High-Interest Savings Accounts (HISAs)
A high-interest savings account (HISA) is amongst the safest investments AND they offer instant access to your cash (no locking it in for a specific period of time).
Big banks offer dismal interest rates of 0.1-0.5% on their savings accounts, so your best bet is to look at Canada’s best online banks, which offer no-fee accounts. The best high-interest savings account in Canada is the Personal Account from EQ Bank, which offers 4% interest and has zero fees. You can learn more about this account and other offerings from EQ in our EQ Bank Review.
PROS:
- 4% interest on your money
- Instant access – no need to lock in for 30 days, 1 year, or 5 years
- The ability to use the EQ Bank card connected to the account
- Free ATM withdrawals anywhere in Canada
- No foreign exchange fees when you pay for things abroad (on vacation)
- $0 in fees
- $100,000 in automatic CDIC insurance
CONS:
- Interest rate can go down if the Bank of Canada lowers rates
- The EQ Everyday Account doesn’t allow you to write cheques to pay for things
GICs
Guaranteed Investment Certificates (GICs) are secured investments. You’re basically lending money to the issuer for a set time period, at which point you’re guaranteed to get your full investment back. In the meantime, you’re guaranteed regular payments of interest on your loan.
GIC interest rates are either fixed (they’ll stay the same no matter what) or variable (they’ll shift depending on the Prime interest rate). Fixed-rate GICs are a safer investment option because interest rates could fall, taking your variable GIC rates with them. And as of the start of 2025, that’s not a risk you want to take.
EQ Bank offers fixed GIC rates of up to 3.60% (for 5 years). You can read more about EQ Bank GICs and other GIC rates in Canada in our list of the Best GIC rates in Canada for 2025.
PROS:
- No fees
- Your deposit is CIDC insured
- Decent returns
- Fixed rate GICs are protected from market fluctuations
CONS:
- There’s a minimum investment
- If you hold your GICs in a non-registered account, any earnings will be taxed
- Your money is tied up until your GIC reaches maturity—you can’t pull it out early, no matter how badly you need it
Treasury Bills
Treasury bills, or T-bills, are loans to the Canadian government. They’re well known as safe investments because the government is near-guaranteed to pay back its debts. Canadian T-bills are sold at a discount and then redeemed at maturity at their face value. They don’t pay interest in the meantime, but when it’s time to redeem them, you’re guaranteed a profit.
While T-bills are lower yield than many other low risk investments, they have the benefit of being guaranteed by well-established central banks.
T-bills are easy to buy through your Canadian online broker. Qtrade, our preferred online broker, charges $1 per $1000 for T-bill purchases, from a minimum of $24.99 to a maximum of $250.
PROS:
- Extremely low risk investments
- Guaranteed profit
- A range of maturity lengths
- Easy to purchase through an online broker
CONS:
- Minimum investment of $1000
- No dividends or interest payments
- Money is locked in for the length of the bill
Money Market Funds
Money Market Funds are low risk mutual funds that contain high quality, short term money market securities like Government of Canada Treasury Bills, debt instruments, or cash equivalents.
Although money market funds aren’t insured, they’re very safe because they contain very safe underlying securities. However, like any mutual funds, they incur a management fee, which can significantly reduce their returns.
You can purchase Money Market funds from discount brokers such as Qtrade or Questrade, or from a Big Bank discount broker like BMO Investorline.
In 2023 we saw a very similar investment to money market funds hit brokerages. The idea is still to invest in a short-term, ultra-safe asset, but in this case it’s not 3-6 month Treasury Bills, but rather high interest savings accounts. Several ETF companies introduced a product known as a cash ETF.
The basic idea behind these products is to pool together large amounts of money from Canadian investors (through ETFs you can buy and sell on a stock exchange) and then negotiate great high interest savings account rates. For more information check out my article on the Best Cash ETFs in Canada.
PROS:
- Highly liquid
- Stable fixed-income investments
- Many money markets pay dividends
CONS:
- Management fees (MERs) eat into investment earnings
- Minimum investments generally start at $100
Bonds
Buying a bond is essentially lending money to the seller for a set time period in exchange for regular interest payments. They’re like GICs, only without the CDIC insurance.
Now, it’s important to understand two things about buying bonds as a low risk investment:
1) There is a massive range of bonds. An investor can buy bonds in anything from the clean water authority down in Florida, to bonds issued by massive companies like Apple. The vast majority of Canadians only really need to understand bonds from very safe entities like provincial/federal governments, or maybe the most stable companies such as Bell.
2) It is very rare these days for an investor to buy a single bond simply because the mechanics are quite cumbersome. Canada savings bonds used to be a popular investment, but even those are more difficult now. Instead, when most people want to invest in bonds they use a bond ETF. You can see which bond ETFs I like best if you check out my best ETFs in Canada article.
Agencies like Moody’s and Standard and Poor’s monitor the quality of bonds and assign grades to help investors make informed decisions.
Bonds can help protect your portfolio against stock market declines but this is not guaranteed either, as folks who owned bonds in 2023 can attest. For a more in-depth look at different fixed income options, check out my article on bond ETFs vs High Interest Savings Accounts vs GICs.
PROS:
- Stable, fixed income
- Have a rating system to help you determine quality
- Can offset stock value losses
CONS:
- Risk level varies widely (do your research)
- More affected by national interest rates than stocks are
- Some unconventional bonds are harder to sell
Annuities
Annuities are slightly different from most low risk investments on our list. An annuity is an insurance contract in which you pay a set sum in exchange for regular payouts in the future. Payment for an annuity either occurs in one lump sum or set monthly premiums during an accumulation period.
Annuities are designed specifically for retirement-age investors and aren’t appropriate for everyone. During the accumulation period, the money you invest is illiquid and can’t be withdrawn without financial penalties. However, once the payout period begins, your income is guaranteed, either for a set amount of time, or for life, depending on your choice of annuity.
An annuity can be a solid addition to a low risk portfolio, but they’re not for everyone. To learn more about the ins and outs and whether they’re right for you, check out our article on Investing in Annuities.
PROS:
- Guaranteed future payments
CONS:
- Money is inaccessible until the payout period begins
- May require a large amount of cash to purchase
- Annuities involve a number of commissions and fees
- Annuity income will be taxed if they’re not held in a registered investment account
Low Risk Stocks
The phrase “low risk stocks” can be a bit of a misnomer. Obviously, some companies are more stable than others, but in saying that, it doesn’t always mean that their stock prices are immune from volatility. Just ask Bell (BCE) investors who thought they were getting a low risk investment over the years how that’s looking at the moment as their share price is down 10% this year (and much more than that over the past few years).
Now, if I had to pick some mature businesses that I believe are low risk Canadian stocks, I would look at utilities, banks, and shares of other companies that pay out relatively high dividend yields. Even more so than the yield however, I’d be looking at the track record of dividend increases over the past several decades.
I achieved financial independence at a young age, thanks in part to being able to stay the course when times were tough in the markets. I weathered those storms because I had concrete conviction in my portfolio of dividend-paying stocks. You can check out my updated list of the Best Canadian Dividend Growth Stocks and my Dividend Kings List.
You’ll find boringly simple companies such as:
- Canadian National Railway (CNR)
- Fortis Inc. (FTS)
- Emera (EMA)
Over the years, I’ve really benefited from my personal relationship with Mike Heroux, and his unique platform for Canadian dividend investors called Dividend Stocks Rock. You can read my full review of Dividend Stocks Rock for more information.
PROS:
- A reliable income stream
- Low risk stocks are unlikely to fluctuate as much as more volatile stocks
- Preferential tax treatment
CONS:
- Dividends can get cut – just ask the folks who have invested in Algonquin Power & Utilities. That said, careful selection can minimize these risks.

Best 2025 Broker Promo
Up to $150 Sign Up Bonus!
Open an account with Qtrade and get the best broker promo in Canada: $150 in cash back when you fund a new account.
The offer is time limited - get it by clicking below.
Must deposit/transfer at least $1,000 in assets within 60 days. Applies to new clients who open a new Qtrade account by October 31, 2025. Qtrade promo 2025: CLICK FOR MORE DETAILS.
Myth: Sitting in Cash is a Low Risk Investment Opportunity
Let’s first all agree that simply storing large cash sums in a safe (or under the mattress, or in a low-interest chequing account) is not an option. Sure, the dollar amount will never go down, but the value of that cash will be eroded by inflation (each dollar is worth less over time). Idle money loses its purchasing power. Simply storing cash may sound risk-free, but it’s actually a strategy that guarantees loss.
We might have an image of Scrooge McDuck diving into a pool of money as the pinnacle of wealth, but he’s actually a poor money manager. He wasted the vast growth potential of all his money by keeping it locked away in his mansion!
Money must be invested to at least maintain – or better yet, grow – its purchasing power.
The “cash is trash” truism was never proven to be so true as in 2023 when we saw your purchasing power decrease massively (sometimes close to 1% per month) due to inflation. While inflation doesn’t look to be as much of a burden in 2025 as it has been the past couple years, it’s still staying stubbornly high. I don’t know about you, but I personally don’t intend to see 3%+ of my net worth inflated away this year because I had cash sitting in a big bank chequing account.
How to Avoid Losing Money on Investments
The best way to avoid losing money on investments is to have a long time horizon and a diversified portfolio that has balanced portions of high risk investments and low risk investments/instruments.
High risk investments earn you high returns over the long term and the low risk investments can be used for short term savings, for waiting out temporary stock market volatility, and for providing stable returns to smooth out volatility in other parts of your portfolio.
The high risk investments like stocks require longer time horizons because stock market returns can fluctuate a lot year over year. Even though they can dip into negative returns and lose money for a year or two, history shows us that if you stay the course, you’ll see average positive returns over time.
People have different risk tolerance and different investment time horizons. So everyone has their own unique balance between high risk investments and low risk investments. Be aware of your investment needs and make sure that your portfolio reflects them.
When to Buy Safe Investments and When to Take More Risks
Low risk investments are a solid choice if you’re someone who loses sleep over the idea of market ups and downs. If you’d rather avoid all the drama of volatile returns, there’s no shame in building a portfolio made up entirely of relatively safe options. Just keep in mind that while you’re protected from the worst drops, you’re also unlikely to earn more than around 3-4% on your money. (Or slightly more than inflation.)
On the other hand, if you’ve got at least five years before you need to tap into your investment portfolio, it might be worth considering a bit more risk. Yes, you’ll see your returns bounce around from year to year, but over the long haul, you’re often rewarded with stronger growth than a purely conservative approach can offer.
As a group, human beings are generally pretty bad at timing the market and deciding when low risk investments or high risk investments are the way to go. Consequently, I don’t recommend bouncing around and getting in and out of the stock market at different times. Pick an asset allocation for the long haul and stick with it. Understand what the short-term worst case scenario is, and realize that you’re going to see that a few times in your portfolio’s lifetime.
Are There Really Safe Investments in Canada with Good Returns?
If you’re on the hunt for a magical, low-risk investment that somehow dishes out sky-high returns, I can save you some time: It doesn’t exist.
Risk and return are a package deal – if an investment could promise big gains while staying rock-solid safe, everyone would pile in, and the potential for large returns would quickly vanish as the price went up.
That said, Canadian investors do have some solid low risk options to choose from right now. One stand-out is EQ Bank’s high-interest savings account, which offers 3.50% on your cash while letting you withdraw whenever you want.
Compared to the major banks’ checking accounts (which typically pay next to nothing), that’s a massive upgrade. To sweeten the deal, as of 2025, EQ also offers easy access to GICs, Canada’s only 30-day notice accounts, and an EQ Bank Card that allows free withdrawals from ATMs across Canada.
Generally speaking, if you need your money within the next three to five years, something like a GIC or high interest savings accounts is your best bet. You don’t want to leave yourself at mercy of the stock market if you are likely to need to pull the money out in the short term. On the other hand, if you have at least five years until you need that money, then you may want to look at our Canadian dividend stock list for some long-term investment ideas.
Just remember, there’s no such thing as a perfect low risk investment that guarantees high returns. It’s all about balancing your priorities and time horizon.

Best 2025 Broker Promo
Up to $150 Sign Up Bonus!
Open an account with Qtrade and get the best broker promo in Canada: $150 in cash back when you fund a new account.
The offer is time limited - get it by clicking below.
Must deposit/transfer at least $1,000 in assets within 60 days. Applies to new clients who open a new Qtrade account by October 31, 2025. Qtrade promo 2025: CLICK FOR MORE DETAILS.
I've Completed My Million Dollar Journey. Let Me Guide You Through Yours!
Sign up below to get a copy of our free eBook: Can I Retire Yet?